Le programme d'exploration des nombres

Ce programme est une mine d'informations sur les nombres, qu'ils soient entiers, rationnels ou racines carrées d'entiers. Le menu propose 5 options : Entier - Deci>Frac - Modulo - Frac>Deci - Change. Chaque option possède un panneau de commande spécifique constitué d'une ou plusieurs zone de saisie précisant les paramètres variables et de 3 à 5 cases à cocher correspondant aux questions à traiter par l'applet.

Par défaut, c'est l'option Entier qui est proposée. Il faut alors entrer un entier et cocher les questions qui nous intéressent, puis valider. Les possibilités pour les questions sont : décomposition en produit de facteurs premiers, diviseurs et somme aliquote, suite des sommes aliquotes, nombres premiers avec ce nombre, racine carrée. Pour voir un exemple, voyez pour 120 dans les copies d'écran de cette rubrique. Quelques rappels utiles : les diviseurs d'un nombre entier sont ceux qui conduisent à un quotient entier (par exemple 3 est un diviseur de 6 car 6:3=2 mais pas de 5 car 5:3=1,6666...). Lorsqu'on additionne tous les diviseurs d'un entier sauf l'entier lui-même, on trouve la somme aliquote de ses diviseurs (par exemple 12, qui a pour diviseurs aliquotes 1, 2, 3, 4 et 6 a pour somme aliquote 16 et est donc qualifié d'abondant). La suite des sommes aliquotes s'interroge sur les sommes aliquotes des sommes aliquotes, pour voir, entre autre, si notre nombre se rattache à un nombre parfait (égal à sa somme aliquote, comme 28 par exemple). Parmi les nombres premiers avec notre nombre (ceux qui n'ont pas d'autre diviseur commun que 1) il y a les nombre premiers (qui n'ont pas d'autre diviseur aliquote que 1) inférieurs à notre nombre mais il y a aussi d'autres nombres généralement. La racine carrée d'un entier qui n'est pas un carré parfait est un nombre irrationnel (qui ne peut pas se mettre sous la forme d'une fraction) et donc son écriture décimale est toujours non-périodique. Mais il peut s'écrire sous une forme périodique à l'aide de nombres entiers: c'est la décomposition en fraction continue. Par exemple la racine carrée de 2 à une période de 2, les coefficients étant [1 1 2] ce qui signifie que ce nombre est égal à : 1+1/(1+1/(2+1/(1+1/(2+1/(...))))).

L'option Change est un complément de l'option Entier. Vous entrez un entier (par défaut celui qui vient de Entier) et vous choisissez les informations  voulues parmi celles-ci : conversion>base de sortie, Ecriture décimale de l'inverse, Liste des nombres premiers longs inférieurs à ce nombre, Système de numération des mayas et Système de numération des babyloniens. Vous devez entrer une base d'entrée si vous voulez que l'on considère votre nombre dans une base particulière (par défaut : base 10). Vous pouvez entrer une base entre 2 et 61, les chiffres étant 1, 2, ...9, a, b, ...z, A, B, ...Z. La base de sortie doit être renseignée si vous voulez convertir dans une autre base. Dans les copies d'écran, voyez l'exemple de 360 écrit en base 20 : i0 (i vaut 18, c'est donc 18x20+0). Mais l'applet donne d'autres renseignements liés à l'écriture du nombre : l'écriture maya (base 20 modifiée) et l'écriture babylonienne (base 60), mais aussi d'autres renseignement concernant l'inverse du nombre, la question étant de savoir si l'inverse de ce nombre a une écriture "décimale" périodique ou non dans la base de sortie. Par exemple, 1/4 est décimal en base 10 (1/4=0,25) mais peut avoir une écriture décimale illimitée dans une autre base (1/4=0,020202... en base 3). Ces informations sont destinées à examiner si le nombre en question est un nombre premier long ou non, un nombre premier long conduit à une inverse qui s'écrit avec une séquence qui se répète à l'infinie d'une longueur égale au nombre moins 1. Par exemple 7 est un nombre premier long en base 10 car 1/7 s'écrit avec une suite de 6 chiffres qui se répètent jusqu'à l'infini : la suite 142857.

L'option Deci>Frac propose d'écrire sous forme fractionnaire irréductible un nombre rationnel donné par sa partie fixe et la séquence qui se répète (les rationnels ont toujours une écriture périodique). Par exemple, le nombre dont l'écriture décimale illimitée est 12,434343... (une suite ininterrompue de 43) correspond à la fraction 1231/99. Pour entrer ce nombre ici, on entre la partie fixe : 12 et la séquence qui se répète 43, puis on coche la question Ecriture de la fraction irréductible correspondante. Les autres questions sont : Séquences cycliques ayant le même nombre de chiffres, et Différentes séquences avec le même dénominateur. Les deux dernières questions envisagent les différentes possibilités qui peuvent se rencontrer avec des écritures décimales voisines : la 1ère décrit les différentes séquences cycliques qui peuvent se rencontrer avec la longueur de notre nombre. Par exemple, si la séquence est 43, donc si la longueur est 2, il n'y a que 5 séquences cycliques originales possibles : 09 - 18 - 27 - 36 - 45 qui sont associées au nombre premier 11 (division par 11). Les autres séquences à 2 chiffres proviennent d'une combinaison de 11 avec d'autres nombres. La séquence 43 provient d'une combinaison de 11 et 9 d'où le dénominateur 99. La dernière question donne la liste de toutes les suites de chiffres qui peuvent se rencontrer avec le dénominateur trouvé. Par exemple, avec le dénominateur 99 il peut y a voir 53 suites différentes, certaines à 1 chiffre, d'autres à 2 chiffres. Le programme donne les numérateurs des fractions donnant ces séquences de chiffres et aussi leur somme, car il s'observe d'étonnante similarité entre ces sommes qui manifestent des propriétés sous-jacentes souvent mal connues... 

L'option Frac>Deci propose d'écrire sous forme décimale illimitée périodique un nombre rationnel donné par une fraction. Par exemple, le nombre rationnel 12/9 va être écrit 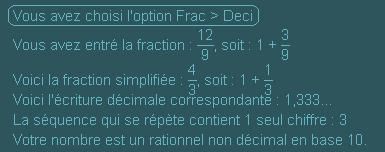1,333... (une infinité de 3). Le programme propose donc tout d'abord l'Ecriture de la fraction irréductible correspondante et l'Ecriture décimale correspondante. Pour notre exemple 12/9, voyez que le programme donne aussi les écritures américaines (partie entière + fraction inférieure à 1). L'écriture décimale précise quelle est la séquence qui se répète et de combien de chiffres elle est composée, ce qui évite de les compter! (voir ci-dessous une illustration pour 12/23). Lorsque la fraction entrée est irréductible, le programme donne les coefficients de Bezout qui permettent d'écrire 1 sous la forme d'une combinaison des deux nombres. Les autres questions traitées dans cette rubrique sont : Fraction continue et Recherche des différentes séquences avec le même dénominateur réduit. La fraction continue est toujours finie pour un rationnel (alors qu'elle est périodique pour la racine carrée d'un entier, voir la rubrique Entier). Par exemple, pour 12/23 elle s'écrit [0 1 1 11] ce qui signifie que 12/23 = 0+1/(1+1/(1+1/11)). Pour les comptabiliser les différentes séquences, le programme commence par les ordonner (en écrivant la permutation circulaire qui conduit au plus petit nombre). Par exemple, la séquence obtenue pour 12/23 est présentée commençant par 0434... qui est en fait la séquence obtenue par l'inverse de 23. La séquence de 12/23 est en fait 12 fois celle de 1/23. Verifiez que 12x04347826... = 521739130...

La dernière option, Modulo, s'intéresse aux écritures des nombres modulo un autre nombre. Par exemple 12 modulo 7 vaut 5 : on enlève autant de fois le modulo qu'il est possible. Ainsi tous les nombres peuvent s'écrire comme leur reste dans la division par le modulo. On trouve cette notion de modulo 7 lorsqu'on s'intéresse au jour de la semaine : quel jour serons-nous dans 12 jours? Le même que dans 5 jours car 12=5 (mod 7). Les opérations usuelles modulo un nombre sont fréquemment employées en arithmétique (étude des nombres entiers). Nous pouvons donc nous intéresser aux Tables d'addition ou aux Tables de multiplication dans un modulo donné. Les tables modulo 7 sont données en exemple. On voit que tous les nombres ont un opposé pour l'addition (cela est vrai pour tous les modulos). L'opposé de 3 est 4 car 3+4=7=0 (mod 7). La table de multiplication modulo 7 montre que chaque nombre a un inverse. Par exemple, l'inverse de 3 est 5 car 3x5=15=1 (mod 7). Cette propriété n'est pas vérifiée par tous les modulos, elle caractérise les nombres premiers. Une autre propriété caractéristique des nombres premiers est visible dans les Tables des puissances : on remarque que toutes les puissances le modulo - 1 sont égales à 1. Cette propriété est un théorème important de l'arithmétique (le petit théorème de Fermat). Il y a d'autres faits intéressants qui permettent de comprendre les caractéristiques de l'écriture décimale d'un rationnel (longueur de la séquence qui se répète, rang de démarrage de la séquence) et qui sont apportés par les puissances de 10, modulo le dénominateur de la fraction. Les développements de ces notions seraient trop longs et existent ailleurs, par exemple dans l'excellent ouvrage de Ian Stewart "Merveilleux nombres premiers". Ainsi donc, les Puissances de votre nombre et le Test factoriel de Wilson sont des notions d'arithmétiques modulaire qui concernent les nombres premiers.